User guide
What you need to know to use this calculator – a step-by-step guide
Our calculator is designed to be easy to use but it does require some understanding of steel beams and structures.
If you need help with any of this, call us on 01332 410066.
1.1) Steel beam span length
This is the effective span length of the beam, the distance from the centre of one end bearing to the centre of the other end bearing. For example, if the clear distance between supports is 3m and the beam has a minimum end bearing length of 0.1m at both ends, you would work out the effective span length as follows:
3m + 0.1m/2 + 0.1m/2 = 3.1m
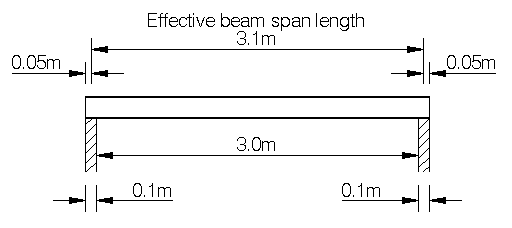
Figure 1A
2.1) Steel beam shape and size
Our calculator defaults to "Universal Beams" but you can also choose "Universal Columns" and "Parallel Flange Channels" as well. Universal Beams and Universal
Columns both have a distinctive "I" shape but whereas the depth and width are very similar in Universal Columns, the depth is always noticeably greater than the
width in a Universal Beam. In contrast, Parallel Flange Channels have a C
shape. Read more about these shapes.
You can also select hollow sections and European sections.
Once you have chosen the right shape of beam, select its dimensions (Depth, Width and Weight) from the Dropdown Menu. If you're not sure what beam size to use, just allow the steel beam calculator to select the beam size for you.
2.2) Select steel grade
Select the steel grade you wish to use, new UK steel is usually S355 grade, older steel is often S275 grade. If you are not sure what grade to use assume the lower S275 grade.
You need to know what type of load your beam will be supporting.
- Uniformly Distributed Load is where the load is evenly distributed across the full length of the beam.
- Partial Uniformly Distributed Load is where the load is evenly distributed across part of the beam.
- Point Load is where there are localised loads at certain points along the beam.
3.1) Uniformly Distributed Loads and Partial Uniformly Distributed Loads
If you choose one of these types, you can select the Loading Details from the Dropdown Menu (e.g. "Sloping roof with an angle of up to 30 degrees or timber floor in a domestic dwelling" and then enter the Width or Height of the load (use "other" if you can't see an option that describes the nature of your load.)
For details on how to calculate the load widths, see our Examples Page and Diagrams showing how to calculate load widths. We also have a list of Standard permanent loads for commonly used items, such as clay tiles and rafters.
You can add multiple loads (e.g. more roofs, floors, walls etc).
You do not need to add the weight of the steel beam itself, our calculator automatically does this.
3.2) Point Loads
If the load on your beam is a Point Load, you will need to enter the dimension between the Point Load and the end of the beam, as well as its Permanent and Variable load.
If you need to work out the point load from a beam which is going to be supported by another beam, please see our How to design a beam which is required to support another beam guide.
4.1) You need to know if the beam is going to be Fully Restrained along its length. Usually, the answer is no. It is only classed as fully restrained if it meets the requirements stated in SCI Publication P360, an example being where a steel beam is cast into a concrete floor. If you need to know more, please call 01332 410066 for help.
If your beam is not going to be fully restrained and the beam is only restrained at its supports, you can select, ‘Unrestrained – the beam is only restrained at its support’.
If the beam is restrained at points along its length, for example where another beam is fixed at right angles to the beam along its length. In this case, you should measure the dimension between the lateral restraint and the beam end and enter this dimension. If there is more than one restraint, you will need to add these as well.
You can also enter a buckling length, for example where the ends of the beams are not fully restrained you can input a buckling length that is greater than the effective span, for more information on buckling lengths please refer to SCI Publication P360. Please call us if you need help.
5.1) Variable load safety factor
Imposed loads (also known as live loads) are usually things that can change, such as people or furniture. In the calculations all the imposed loads are multiplied by this safety factor to ensure a safe design. Recommended value from EN 1990:2002+A1 Eurocode – Basis of structural design (UK National annex) is 1.5 and our Calculator defaults to this.
5.2) Permanent load safety factor
Permanent loads (also known as dead loads) are usually things that do not change, such as the weight of the floor or a wall. In the calculations all the permanent loads are multiplied by this safety factor to ensure a safe design. Recommended value from EN 1990:2002+A1 Eurocode – Basis of structural design (UK National annex) is 1.35 and our Calculator defaults to this.
5.3) Moment gradient factor C1
Recommended C1 value is 1. This is the most conservative, safe value and is recommended for general use. The distribution of bending moments along the length of the beam affects it buckling capacity, C1 is a factor for the shape of the bending moment between points of lateral restraint, for a beam with only uniformly distributed loads along its full length C1 can be taken as 1.13, for more information see SCI Publication P360.
A Deflection Limit is the maximum amount you allow the beam to sag. You can set a limit for how much it can sag under Variable Loads – usually things that can change, such as people or furniture – and under Permanent Loads, such as the weight of the floor or a wall. Our Calculator defaults to the recommended limits, but you may need to change these.
6.1) Variable Load Deflection Limit
Normally this is restricted to span/360, however there are exceptions. For example, if you are using the beam to span above bi-fold doors you may need to set a lower limit, or if the beam is going to be used as a structural ridge beam the variable load deflection should not normally exceed 10mm.
6.2) Total Variable and Permanent Load Deflection Limit
We recommend this is usually span/200, however, some engineers recommend span/250.
That’s all the information we need. Now you just have to press the ‘Run Calculation’ button and your PDF report will appear in seconds. If you are using the auto select feature, you will be shown a list of all the steel beam sizes that are suitable for your requirements.
Further Guidance
StabilityStability is critically important, sometimes when removing a load bearing wall you will need to install a steel type goalpost type arrangement where the steel beam is supported at both ends by steel posts. This is generally only required if there is insufficient masonry for the building to remain stable.
If the geometry of the masonry complies with the guidance in Regulations Approved Document A, steel goal posts will not generally be required. If steel goal posts are required and you are not competent to design them, we would recommend that you employ an experienced Structural Engineer to design these for you.
Destabilising loads
A description of a destabilising load would be a free standing wall on top of a steel beam. Generally in domestic buildings free standing walls are infrequent. Walls are either fixed via roofs or floors and buttressing walls at right angles to the wall will provide further restraint.
If the wall above the beam is unrestrained, the wall will be deemed unstable and would be classed as a dangerous structure in need of urgent attention and repair. It is therefore generally considered that in domestic buildings walls are not destabilising loads. Loads from roofs and floors are structural elements that provide resistance to lateral (horizontal) movement and are not destabilising loads.
More tools from us
We also offer:For help interpreting and using these please call us: 01332 410066.

 USA
USA
 Eurocode
Eurocode

 United Kingdom
United Kingdom